Combinatorial Aspects of [Colored] Point Sets in the Plane

B. Vogtenhuber

Abstract:

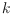
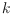
Combinatorial geometry and graph theory are both areas in the field of discrete mathematics. The study of combinatorial aspects of point sets in the plane and graphs based on them is situated in the intersection of these areas and also includes aspects of computational geometry and graph drawing. We study variations of the classical Erdos-Szekeres problems on convex $k$-gons and $k$-holes. 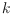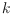Relaxing the convexity condition, we show structural results and bounds on the numbers of $k$-gons and $k$-holes. 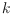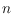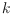Most noteworthy, for constant $k$ and sufficiently large $n$, we give a quadratic lower bound for the number of $k$-holes and show that this number is maximized by sets in convex position. For bichromatic point sets, we show that every sufficiently large such set contains a monochromatic 4-hole. Continuing with investigations on bichromatic point sets, a famous problem is Zarankiewicz's conjecture on the crossing number of the complete bipartite graph. Studying rectilinear versions of this conjecture, we present several interesting observations. The main question remains unsettled even for these variations though. We also consider the existence of different kinds of compatible colored matchings for given bichromatic graphs of certain classes and present bounds on their cardinalities. The study of Delaunay triangulations is a central topic in geometric graph theory. 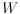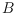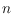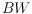We investigate the question of finding a set of additional points $W$ for a given set $B$ with $n$ points such that the Delaunay triangulation of the joint set $B\dunion W$ does not contain any edge spanned by two points of $B$. 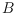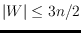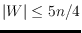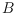Improving the previously best known bounds, we show that $\vert W\vert\leq3n/2$ points are sufficient in general and $\vert W\vert\leq5n/4$ points suffice if $B$ is a convex set. We also present a lower bound of $\vert W\vert\geq n-1$. 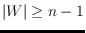Investigating pointed pseudo-triangulations, we study the existence of compatible pointed pseudo-triangulations whose union is a maximal plane graph. We present a construction for pairs of such pseudo-triangulations for a given point set. A given pointed pseudo-triangulation in general does not admit such a compatible pseudo-triangulation. Finally, we generalize the pointedness property of pointed pseudotriangulations to other types of graphs. We consider (1) redrawing the edges of a given plane straight-line graph such that all vertices become pointed; and (2) embedding a planar graph such that every vertex has all its incident edges within a small angle. We show that both tasks can be realized using Bézier-curves, biarcs or polygonal chains of length two as edges.

Reference: B. Vogtenhuber. Combinatorial Aspects of [Colored] Point Sets in the Plane. PhD thesis, Institute for Software Technology, Graz University of Technology, Graz, Austria, December 2011. Supervisor: Oswin Aichholzer.