Empty Rainbow Triangles in k-colored Point Sets

R. Fabila-Monroy, D. Perz, and A. L. Trujillo

Abstract:

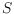
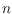
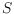
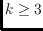
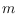
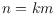
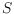
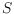
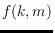
Let $S$ be a set of $n$ points in general position in the plane. Suppose that each point of $S$ has been assigned one of $k \ge 3$ possible colors and that there is the same number, $m$, of points of each color class, so $n=km$. A triangle with vertices on $S$ is empty if it does not contain points of $S$ in its interior and it is rainbow if all its vertices have different colors. Let $f(k,m)$ be the minimum number of empty rainbow triangles determined by $S$. 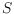In this paper we show that $f(k,m)=\Theta(k^3)$. 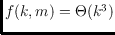Furthermore we give a construction which does not contain an empty rainbow quadrilateral.

Reference: R. Fabila-Monroy, D. Perz, and A. L. Trujillo. Empty rainbow triangles in k-colored point sets. In Proceedings of the 36th European Workshop on Computational Geometry (EuroCG$\,$2020), Würzburg, Germany, 2020.