Routing in Simple Polygons

M. Korman, W. Mulzer, A. van Renssen, M. Roeloffzen, P. Seiferth, Y. Stein, B. Vogtenhuber, and M. Willert

Abstract:

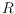
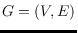
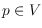
A routing scheme $R$ in a network $G=(V,E)$ is an algorithm that allows to send messages from one node to another in the network. We are first allowed a preprocessing phase in which we assign a unique label to each node $p\in V$ and a routing table with additional information. After this preprocessing, the routing algorithm itself must be local (i.e., we can only use the information from the label of the target and the routing table of the node that we are currently at). 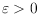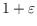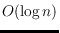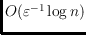We present a routing scheme for routing in simple polygons: for any $\varepsilon > 0$ the routing scheme provides a stretch of $1+\varepsilon$, labels have $O(\log n)$ bits, the corresponding routing tables are of size $O(\varepsilon^{-1}\log n)$, and the preprocessing time is $O(n^2+\varepsilon^{-1}n)$. 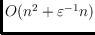This improves the best known strategies for general graphs by Roditty and Tov (Distributed Computing 2016).

Reference: M. Korman, W. Mulzer, A. van Renssen, M. Roeloffzen, P. Seiferth, Y. Stein, B. Vogtenhuber, and M. Willert. Routing in simple polygons. In Proc. $33^{rd}$ European Workshop on Computational Geometry EuroCG '17, pages 17-20, Malmö, Sweden, 2017.