The dual diameter of triangulations

M. Korman, S. Langerman, W. Mulzer, A. Pilz, M. Saumell, and B. Vogtenhuber

Abstract:

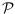
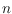
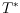
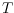
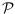
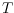
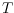
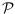
Let $\mathcal{P}$ be a simple polygon with $n$ vertices. The dual graph $T^*$ of a triangulation $T$ of $\mathcal{P}$ is the graph whose vertices correspond to the bounded faces of $T$ and whose edges connect those faces of $T$ that share an edge. We consider triangulations of $\mathcal{P}$ that minimize or maximize the diameter of their dual graph. 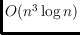We show that both triangulations can be constructed in $O(n^3\log n)$ time using dynamic programming. 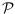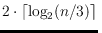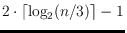If $\mathcal{P}$ is convex, we show that any minimizing triangulation has dual diameter exactly $2\cdot\lceil\log_2(n/3)\rceil$ or $2\cdot\lceil\log_2(n/3)\rceil -1$, depending on $n$. 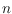Trivially, in this case any maximizing triangulation has dual diameter $n-2$. 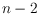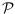Furthermore, we investigate the relationship between the dual diameter and the number of ears (triangles with exactly two edges incident to the boundary of $\mathcal{P}$) in a triangulation. 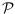For convex $\mathcal{P}$, we show that there is always a triangulation that simultaneously minimizes the dual diameter and maximizes the number of ears. In contrast, we give examples of general simple polygons where every triangulation that maximizes the number of ears has dual diameter that is quadratic in the minimum possible value. We also consider the case of point sets in general position in the plane. 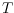of $T$ is defined as before. 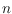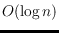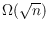We show that for any such set of $n$ points there are triangulations with dual diameter in $O(\log n)$ and in  $\Omega(\sqrt n)$.

Reference: M. Korman, S. Langerman, W. Mulzer, A. Pilz, M. Saumell, and B. Vogtenhuber. The dual diameter of triangulations. Computational Geometry: Theory and Applications, 68:243-252, 2018. Special Issue in Memory of Ferran Hurtado.