Lombardi Drawings of Knots and Links

P. Kindermann, S. Kobourov, M. Löffler, M. Nöllenburg, A. Schulz, and B. Vogtenhuber

Abstract:

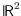
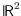
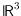
Knot and link diagrams are projections of one or more 3-dimensional simple closed curves into ${{\sf l} \kern -.10em {\sf R} }^2$, such that no more than two points project to the same point in ${{\sf l} \kern -.10em {\sf R} }^2$. These diagrams are drawings of 4-regular plane multigraphs. 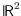Knots are typically smooth curves in ${{\sf l} \kern -.10em {\sf R} }^3$, so their projections should be smooth curves in ${{\sf l} \kern -.10em {\sf R} }^2$ with good continuity and large crossing angles: exactly the properties of Lombardi graph drawings (defined by circular-arc edges and perfect angular resolution). We show that several knots do not allow plane Lombardi drawings. On the other hand, we identify a large class of 4-regular plane multigraphs that do have Lombardi drawings. We then study two relaxations of Lombardi drawings and show that every knot admits a plane 2-Lombardi drawing (where edges are composed of two circular arcs). 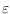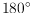Further, every knot is near-Lombardi, that is, it can be drawn as Lombardi drawing when relaxing the angular resolution requirement by an arbitrary small angular offset $\varepsilon$, while maintaining a $180^\circ$ angle between opposite edges.

Reference: P. Kindermann, S. Kobourov, M. Löffler, M. Nöllenburg, A. Schulz, and B. Vogtenhuber. Lombardi drawings of knots and links. In F. Frati and K.-L. Ma, editors, Graph Drawing and Network Visualization. GD 2017., pages 113-126, Boston, MA, USA, 2018. Springer, Cham. Revised Selected Papers.