On weighted sums of numbers of convex polygons in point sets

C. Huemer, D. Oliveros, P. Pérez-Lantero, F. Torra, and B. Vogtenhuber

Abstract:

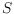
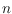
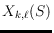
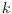
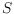
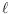
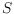
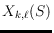
Let $S$ be a set of $n$ points in general position in the plane, and let $X_{k,\ell}(S)$ be the number of convex $k$-gons with vertices in $S$ that have exactly $\ell$ points of $S$ in their interior. We prove several equalities for the numbers $X_{k,\ell}(S)$. This problem is related to the Erdos-Szekeres theorem. Some of the obtained equations also extend known equations for the numbers of empty convex polygons to polygons with interior points. Analogous results for higher dimension are shown as well.

Reference: C. Huemer, D. Oliveros, P. Pérez-Lantero, F. Torra, and B. Vogtenhuber. On weighted sums of numbers of convex polygons in point sets. submitted, pages 1-23, 2019.