New results on minimum-weight triangulations and the LMT skeleton

R. Hainz, O. Aichholzer, and F. Aurenhammer

Abstract:

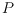
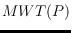
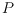
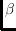
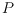
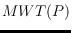
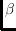
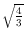
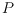
Let $P$ be a simple polygon in the plane and let $MWT(P)$ be a minimum-weight triangulation of $P$. We prove that the $\beta$-skeleton of $P$ is a subset of $MWT(P)$ for all values $\beta$ > $\sqrt{\frac{4}{3}}$ provided $P$ is convex or near-convex. This settles the question of tightness of this bound for a special case and gives evidence for its validity in the general point set case.
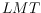
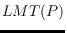
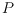
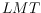
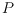
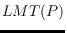
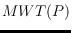
We further disprove the conjecture that the so-called $LMT$-skeleton coincides with the intersection of all locally minimal triangulations, $LMT(P)$, even for convex polygons $P$. We introduce an improved $LMT$-skeleton algorithm which, for simple polygons $P$, exactly computes $LMT(P)$, and thus a larger subgraph of $MWT(P)$. 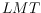The algorithm achieves the same in the general point set case provided the connectedness of the improved $LMT$-skeleton, which is given in allmost all practical instances.

Reference: R. Hainz, O. Aichholzer, and F. Aurenhammer. New results on minimum-weight triangulations and the LMT skeleton. In Proc. $13^{th}$ European Workshop on Computational Geometry CG '97, pages 4-6, Würzburg, Germany, 1997.