The relaxation of triangulations to pseudo-triangulations is already well
known. We investigate the differences between triangulations and
pseudo-triangulations with respect to the optimality criterion of minimal
total edge length. We show that, although (especially pointed)
pseudo-triangulations have significantly less edges than triangulations, the
minimum weight pseudo-triangulation can be a triangulation in general. We
study the flip graphs for pseudo-triangulations whose maximum vertex degree
is bounded by some constant. For point sets in convex position, we prove that
the flip graph of such pseudo-triangulations is connected if and only if the
degree bound is larger than 6. We present an upper bound of
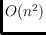
on the
diameter of this flip graph and also discuss point sets in general position.
Finally we relax triangulations even beyond the concept of
pseudo-triangulations and introduce the class of pre-triangulations. When
considering liftings of triangulations in general polygonal domains and
flipping therein, pre-triangulations arise naturally in three different
contexts: When characterizing polygonal complexes that are liftable to
three-space in a strong sense, in flip sequences for general liftable
polygonal complexes, and as graphs of maximal locally convex functions.