Let S be a set of n points in general position in the plane. Suppose that each
point of S has been assigned one of
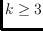
possible colors and that there
is the same number, m, of points of each color class. This means n=km. A
polygon with vertices on S is empty if it does not contain points of S in its
interior; and it is rainbow if all its vertices have different colors. Let
f(k,m) be the minimum number of empty rainbow triangles determined by S. In
this paper we give tight asymptotic bounds for this function. Furthermore, we
show that S may not determine an empty rainbow quadrilateral for some
arbitrarily large values of k and m.