Perfect rainbow polygons for colored point sets in the plane

D. Flores-Peñaloza, M. Kano, L. Martínez-Sandoval, D. Orden, J. Tejel, C. D. Tóth, J. Urrutia, and B. Vogtenhuber

Abstract:

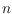
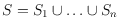
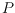
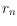
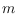
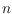
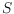
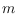
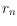
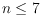
Given a planar $n$-colored point set $S= S_1 \cup \ldots \cup S_n$ in general position, a simple polygon $P$ is called a perfect rainbow polygon if it contains exactly one point of each color. The rainbow index $r_n$ is the minimum integer $m$ such that every $n$-colored point set $S$ has a perfect rainbow polygon with at most $m$ vertices. 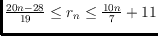We determine the values of $r_n$ for $n \leq 7$, and prove that in general $\frac{20n-28}{19} \leq r_n \leq \frac{10n}{7} + 11$.

Reference: D. Flores-Peñaloza, M. Kano, L. Martínez-Sandoval, D. Orden, J. Tejel, C. D. Tóth, J. Urrutia, and B. Vogtenhuber. Perfect rainbow polygons for colored point sets in the plane. In Proc. XVIII Encuentros de Geometría Computacional, pages 43-46, Girona, Spain, 2019.