Minimizing The Maximum Distance Traveled To Form Patterns With Systems
of Mobile Robots
J. Coleman, E. Kranakis, O. M. Ponce, J. Opatrny, J. Urrutia, and
B. Vogtenhuber
Abstract:
In the pattern formation problem, robots in a system must self-coordinate to
form a given pattern, regardless of translation, rotation, uniform-scaling,
and/or reflection. In other words, a valid final configuration of the system
is a formation that is similar to the desired pattern. While there has been
no shortage of research in the pattern formation problem under a variety of
assumptions, models, and contexts, we consider the additional constraint that
the maximum distance traveled among all robots in the system is minimum.
Existing work in pattern formation and closely related problems are typically
application-specific or not concerned with optimality (but rather
feasibility). We show the necessary conditions any optimal solution must
satisfy and present a solution for systems of three robots. Our work also led
to a surprising result that has applications beyond pattern formation.
Namely, a metric for comparing two triangles where a distance of 0 indicates
the triangles are similar, and 1 indicates they are fully dissimilar.
Reference: J. Coleman, E. Kranakis, O. M. Ponce, J. Opatrny, J. Urrutia,
and B. Vogtenhuber.
Minimizing the maximum distance traveled to form patterns with systems of
mobile robots.
In Proc. 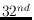 Annual Canadian Conference on Computational Geometry
CCCG 2020, pages 73-79, Saskatoon, Saskatchewan, Canada, 2020.
Annual Canadian Conference on Computational Geometry
CCCG 2020, pages 73-79, Saskatoon, Saskatchewan, Canada, 2020.
www-data,
2021-02-10