Evacuating Robots from a Disk Using Face-to-Face Communication

J. Czyzowicz, K. Georgiou, E. Kranakis, L. Narayanan, J. Opatrny, and B. Vogtenhuber

Abstract:

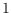
Assume that two robots are located at the centre of a unit disk. Their goal is to evacuate from the disk through an exit at an unknown location on the boundary of the disk. At any time the robots can move anywhere they choose on the disk, independently of each other, with maximum speed $1$. The robots can cooperate by exchanging information whenever they meet. We study algorithms for the two robots to minimize the evacuation time: the time when both robots reach the exit. Czyzowicz et al. 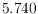(2014) gave an algorithm defining trajectories for the two robots yielding evacuation time at most $5.740$ and also proved that any algorithm has evacuation time at least $3+ \frac{\pi}{4} + \sqrt{2} \approx 5.199$. 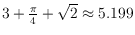We improve both the upper and lower bound on the evacuation time of a unit disk. 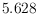Namely, we present a new non-trivial algorithm whose evacuation time is at most $5.628$ and show that any algorithm has evacuation time at least $3+ \frac{\pi}{6} + \sqrt{3} \approx 5.255$. 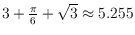To achieve the upper bound, we designed an algorithm which proposes a forced meeting between the two robots, even if the exit has not been found by either of them. We also show that such a strategy is provably optimal for a related problem of searching for an exit placed at the vertices of a regular hexagon.

Reference: J. Czyzowicz, K. Georgiou, E. Kranakis, L. Narayanan, J. Opatrny, and B. Vogtenhuber. Evacuating robots from a disk using face-to-face communication. Discrete Mathematics & Theoretical Computer Science, 22(4), 2020.