Nearest-Neighbor Decompositions of Drawings

J. Cleve, N. Grelier, K. Knorr, M. Löffler, W. Mulzer, and D. Perz

Abstract:

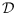
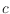
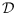
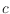
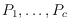
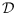
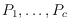
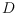
Let $\mathcal{D}$ be a straight-line drawing of a graph in the plane, and let $c$ be a positive integer. We say that $\mathcal{D}$ has a nearest-neighbor decomposition into $c$ parts if there are point sets $P_1, \dots, P_c$ such that $\mathcal{D}$ is the union of the nearest neighbor graphs on $P_1, \dots, P_c$. 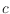We study the complexity of deciding whether it is possible to draw $D$ as the union of $c$ nearest-neighbor graphs.

Reference: J. Cleve, N. Grelier, K. Knorr, M. Löffler, W. Mulzer, and D. Perz. Nearest-neighbor decompositions of drawings. In Proceedings of the 37th European Workshop on Computational Geometry (EuroCG$\,$2021), St. Petersburg, Germany, 2021.