Coloring Circle Arrangements: New 4-Chromatic Planar Graphs

M.-K. Chiu, S. Felsner, M. Scheucher, F. Schröder, R. Steiner, and B. Vogtenhuber

Abstract:

Felsner, Hurtado, Noy and Streinu (2000) conjectured that arrangement graphs of simple great-circle arrangements have chromatic number at most 3. This paper is motivated by the conjecture. We show that the conjecture holds in the special case when the arrangement is 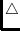$\triangle$-saturated, i.e., arrangements where one color class of the 2-coloring of faces consists of triangles only. 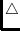Moreover, we extend $\triangle$-saturated arrangements with certain properties to a family of arrangements which are 4-chromatic. The construction has similarities with Koester's (1985) crowning construction. We also investigate fractional colorings. 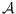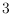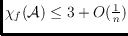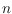We show that every arrangement $\mathcal{A}$ of pairwise intersecting pseudocircles is “close” to being $3$-colorable; more precisely $\chi_f(\mathcal{A}) \le 3+O(\frac{1}{n})$ where $n$ is the number of pseudocircles. 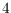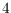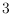Furthermore, we construct an infinite family of $4$-edge-critical $4$-regular planar graphs which are fractionally $3$-colorable. 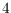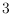This disproves the conjecture of Gimbel, Kündgen, Li and Thomassen (2019) that every $4$-chromatic planar graph has fractional chromatic number strictly greater than $3$.

Reference: M.-K. Chiu, S. Felsner, M. Scheucher, F. Schröder, R. Steiner, and B. Vogtenhuber. Coloring circle arrangements: New 4-chromatic planar graphs. In J. Nešetril, G. Perarnau, J. Rué, and O. Serra, editors, Extended Abstracts EuroComb 2021, pages 84-91, Cham, 2021. Springer International Publishing.