Routing in polygonal domains

B. Banyassady, M.-K. Chiu, M. Korman, W. Mulzer, A. van Renssen, M. Roeloffzen, P. Seiferth, Y. Stein, B. Vogtenhuber, and M. Willert

Abstract:

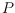
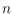
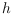
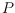
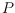
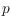
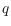
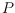
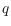
We consider the problem of routing a data packet through the visibility graph of a polygonal domain $P$ with $n$ vertices and $h$ holes. We may preprocess $P$ to obtain a label and a routing table for each vertex of $P$. Then, we must be able to route a data packet between any two vertices $p$ and $q$ of $P$, where each step must use only the label of the target node $q$ and the routing table of the current node. 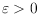For any fixed $\varepsilon>0$, we present a routing scheme that always achieves a routing path whose length exceeds the shortest path by a factor of at most $1+\varepsilon$. 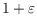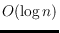The labels have $O(\log n)$ bits, and the routing tables are of size $O((\varepsilon-1+h)\log n)$. 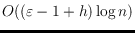The preprocessing time is $O(n^2 \log n)$. 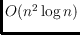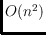It can be improved to $O(n^2)$ for simple polygons.

Reference: B. Banyassady, M.-K. Chiu, M. Korman, W. Mulzer, A. van Renssen, M. Roeloffzen, P. Seiferth, Y. Stein, B. Vogtenhuber, and M. Willert. Routing in polygonal domains. Computational Geometry, 87:101593, 2020. Special Issue on the 33rd European Workshop on Computational Geometry.