We consider an Erdos type question on
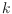
-holes (empty
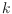
-gons) in
bichromatic point sets. For a bichromatic point set
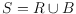
, a
balanced
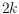
-hole in
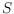
is spanned by
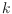
points of
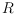
and
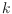
points of
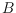
. We show that if
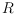
and
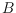
are linearly separable and
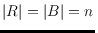
,
then the number of balanced 6-holes in
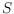
is at least
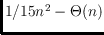
.