Pointed Drawings of Planar Graphs

O. Aichholzer, G. Rote, A. Schulz, and B. Vogtenhuber

Abstract:

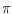
We study the problem how to draw a planar graph such that every vertex is incident to an angle greater than $\pi$. In general a straight-line embedding cannot guarantee this property. We present algorithms which construct such drawings with either tangent-continuous biarcs or quadratic Bézier curves (parabolic arcs), even if the positions of the vertices are predefined by a given plane straight-line embedding of the graph. Moreover, the graph can be embedded with circular arcs if the vertices can be placed arbitrarily. The topic is related to non-crossing drawings of multigraphs and vertex labeling.

Reference: O. Aichholzer, G. Rote, A. Schulz, and B. Vogtenhuber. Pointed drawings of planar graphs. In Proc. $19th$ Annual Canadian Conference on Computational Geometry CCCG 2007, pages 237-240, Ottawa, Ontario, Canada, 2007.