The Zigzag Path of a Pseudo-Triangulation

O. Aichholzer, G. Rote, B. Speckmann, and I. Streinu

Abstract:

We define the zigzag path of a pseudo-triangulation, a concept generalizing the path of a triangulation of a point set. The pseudo-triangulation zigzag path allows us to use divide-and-conquer type of approaches for suitable (i.e., decomposable) problems on pseudo-triangulations. 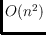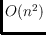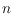For this we provide an algorithm that enumerates all pseudo-triangulation zigzag paths (of all pseudo-triangulations of a given point set with respect to a given line) in $O(n^2)$ time per path and $O(n^2)$ space, where $n$ is the number of points. We illustrate applications of our scheme which include a novel algorithm to count the number of pseudo-triangulations of a point set.

Reference: O. Aichholzer, G. Rote, B. Speckmann, and I. Streinu. The zigzag path of a pseudo-triangulation. In Lecture Notes in Computer Science, Proc. 8th International Workshop on Algorithms and Data Structures (WADS), volume 2748, pages 377-389, 2003.