A quadratic distance bound on sliding between crossing-free spanning trees - Extended Abstract

O. Aichholzer and K. Reinhardt

Abstract:

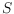
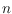
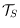
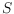
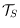
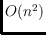
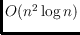
Let $S$ be a set of $n$ points in the plane and let ${\mathcal T}_S$ be the set of all crossing-free spanning trees of $S$. We show that any two trees in ${\mathcal T}_S$ can be transformed into each other by $O(n^2)$ local and constant-size edge slide operations. No polynomial upper bound for this task has been known, but in [#!AAH!#] a bound of $O(n^2 \log n)$ operations was conjectured.

Reference: O. Aichholzer and K. Reinhardt. A quadratic distance bound on sliding between crossing-free spanning trees - extended abstract. In Proc. $20^{th}$ European Workshop on Computational Geometry EWCG '04, pages 13-16, Sevilla, Spain, 2004.