Shooting Stars in Simple Drawings of $K_{m,n}$

O. Aichholzer, I. Parada, M. Scheucher, B. Vogtenhuber, and A. Weinberger

Abstract:

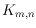
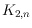
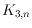
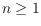
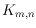
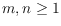
In this work we study the existence of plane spanning trees in simple drawings of the complete bipartite graph $K_{m,n}$. We show that every simple drawing of $K_{2,n}$ and $K_{3,n}$, $n \geq 1$, as well as every outer drawing of $K_{m,n}$ for any $m,n \geq 1$, contains plane spanning trees. Moreover, for all these cases we show the existence of special plane spanning trees, which we call shooting stars. Shooting stars are spanning trees that contain the star of a vertex, i.e., all its incident edges.

Reference: O. Aichholzer, I. Parada, M. Scheucher, B. Vogtenhuber, and A. Weinberger. Shooting stars in simple drawings of $k_{m,n}$. In Proc. $35^{th}$ European Workshop on Computational Geometry EuroCG '19, pages 59:1-59:6, Utrecht, The Netherlands, 2019.