We study a variation of the well known Hadwiger-Nelson problem on the
chromatic number of the Euclidean plane. An embedding of a given triangle
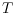
into the colored plane is called monochromatic, if the three corners of the
triangle get the same color. We provide a classification of triangles
according to the number of colors needed to color the plane so that the
triangle can not be embedded monochromatically. For example, we show that for
near-equilateral triangles three colors are enough and that for almost all
triangles six colors are sufficient.