On the Number of Pseudo-Triangulations of Certain Point Sets

O. Aichholzer, D. Orden, F. Santos, and B. Speckmann

Abstract:

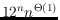
We pose a monotonicity conjecture on the number of pseudo-triangulations of any planar point set, and check it on two prominent families of point sets, namely the so-called double circle and double chain. The latter has asymptotically $12^n n^{\Theta(1)}$ pointed pseudo-triangulations, which lies significantly above the maximum number of triangulations in a planar point set known so far.

Reference: O. Aichholzer, D. Orden, F. Santos, and B. Speckmann. On the number of pseudo-triangulations of certain point sets. Journal of Combinatorial Theory, Series A, 115(2):254-278, 2008.