On the Structure of sets attaining the rectilinear crossing number

O. Aichholzer, D. Orden, and P. Ramos

Abstract:

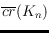
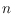
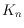
We study the structural properties of the point configurations attaining the rectilinear crossing number $\overline{cr}(K_n)$, that is, those $n$-point sets that minimize the number of crossings over all possible straight-edge embeddings of $K_n$ in the plane. As a main result we prove the conjecture that such sets always have a triangular convex hull. 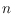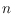The techniques developed allow us to show a similar result for the halving-edge problem: For any $n$ there exists a set of $n$ points with triangular convex hull that maximizes the number of halving edges. 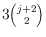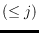Moreover, we provide a simpler proof of the following result: any set of points in the plane in general position has at least $3{j+2 \choose 2}$ $(\leq j)$-edges. This bound is known to be tight for $0\leq j\leq \lfloor\frac{n}{3}\rfloor-1$. 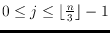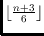In addition, we show that for point sets achieving this bound the $\lfloor\frac{n+3}{6}\rfloor$ outermost convex layers are triangles.

Reference: O. Aichholzer, D. Orden, and P. Ramos. On the structure of sets attaining the rectilinear crossing number. In Proc. $22^{nd}$ European Workshop on Computational Geometry EuroCG '06, pages 43-46, Delphi, Greece, 2006.