Disjoint Compatibility via Graph Classes

O. Aichholzer, J. Obmann, P. Paták, D. Perz, J. Tkadlec, and B. Vogtenhuber

Abstract:

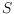
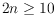
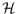
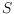
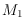
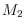
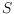
Two plane drawings of graphs on the same set of points are called disjoint compatible if their union is plane and they do not have an edge in common. Let $S$ be a convex point set of $2n \geq 10$ points and let $\mathcal{H}$ be a family of plane drawings on $S$. 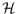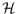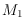Two plane perfect matchings $M_1$ and $M_2$ on $S$ (which do not need to be disjoint nor compatible) are disjoint $\mathcal{H}$-compatible if there exists a drawing in $\mathcal{H}$ which is disjoint compatible to both $M_1$ and $M_2$. 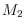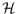In this work, we consider the graph which has all plane perfect matchings as vertices and where two vertices are connected by an edge if the matchings are disjoint $\mathcal{H}$-compatible. We study the diameter of this graph when $\mathcal{H}$ is the family of all plane spanning trees, caterpillars or paths. We show that in the first two cases the graph is connected with constant and linear diameter, respectively, while in the third case it is disconnected.

Reference: O. Aichholzer, J. Obmann, P. Paták, D. Perz, J. Tkadlec, and B. Vogtenhuber. Disjoint compatibility via graph classes. In M. A. Bekos and M. Kaufmann, editors, Graph-Theoretic Concepts in Computer Science. WG 2022., volume 13453 of Lecture Notes in Computer Science (LNCS), pages 16-28, Cham, 2022. Springer International Publishing.