Disjoint tree-compatible plane perfect matchings

O. Aichholzer, J. Obmann, P. Paták, D. Perz, and J. Tkadlec

Abstract:

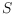
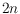
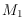
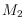
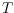
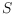
Two plane drawings of geometric graphs on the same set of points are called disjoint compatible if their union is plane and they do not have an edge in common. 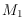For a given set $S$ of $2n$ points two plane drawings of perfect matchings $M_1$ and $M_2$ (which do not need to be disjoint nor compatible) are disjoint tree-compatible if there exists a plane drawing of a spanning tree $T$ on $S$ which is disjoint compatible to both $M_1$ and $M_2$. 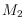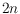We show that the graph of all disjoint tree-compatible perfect geometric matchings on $2n$ points in convex position is connected if and only if $2n \geq 10$. 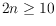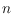Moreover, in that case the diameter of this graph is either 4 or 5, independent of $n$.

Reference: O. Aichholzer, J. Obmann, P. Paták, D. Perz, and J. Tkadlec. Disjoint tree-compatible plane perfect matchings. In Proceedings of the 36th European Workshop on Computational Geometry (EuroCG$$2020), pages 56:1-56:7, Würzburg, Germany, 2020.