NP-Completeness of Max-Cut for Segment Intersection Graphs

O. Aichholzer, W. Mulzer, P. Schnider, and B. Vogtenhuber

Abstract:

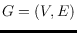
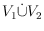
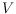
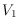
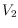
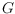
We consider the problem of finding a maximum cut in a graph $G = (V, E)$, that is, a partition $V_1 \dot\cup V_2$ of $V$ such that the number of edges between $V_1$ and $V_2$ is maximum. It is well known that the decision problem whether $G$ has a cut of at least a given size is in general NP-complete. We show that this problem remains hard when restricting the input to segment intersection graphs. These are graphs whose vertices can be drawn as straight-line segments, where two vertices share an edge if and only if the corresponding segments intersect. We obtain our result by a reduction from a variant of PLANAR MAX-2-SAT that we introduce and also show to be NP-complete.

Reference: O. Aichholzer, W. Mulzer, P. Schnider, and B. Vogtenhuber. Np-completeness of max-cut for segment intersection graphs. In Proc. $34^{th}$ European Workshop on Computational Geometry EuroCG '18, pages 32:1-32:6, Berlin, Germany, 2018.