Let
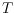
be a triangulation of a simple polygon. A
flip in
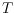
is the
operation of replacing one diagonal of
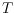
by a different one such that the
resulting graph is again a triangulation. The
flip distance between
two triangulations is the smallest number of flips required to transform one
triangulation into the other. For the special case of convex polygons, the
problem of determining the shortest flip distance between two triangulations
is equivalent to determining the rotation distance between two binary trees,
a central problem which is still open after over 25 years of intensive study.
We show that computing the flip distance between two triangulations of a
simple polygon is NP-hard. This complements a recent result that shows
APX-hardness of determining the flip distance between two triangulations of a
planar point set.