Flip Distance between Triangulations of a Simple Polygon is NP-Complete

O. Aichholzer, W. Mulzer, and A. Pilz

Abstract:

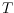
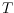
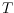
Let $T$ be a triangulation of a simple polygon. A flip in $T$ is the operation of replacing one diagonal of $T$ by a different one such that the resulting graph is again a triangulation. The flip distance between two triangulations is the smallest number of flips required to transform one triangulation into the other. For the special case of convex polygons, the problem of determining the shortest flip distance between two triangulations is equivalent to determining the rotation distance between two binary trees, a central problem which is still open after over 25 years of intensive study. We show that computing the flip distance between two triangulations of a simple polygon is NP-hard. This complements a recent result that shows APX-hardness of determining the flip distance between two triangulations of a planar point set.

Reference: O. Aichholzer, W. Mulzer, and A. Pilz. Flip distance between triangulations of a simple polygon is NP-complete. In Proc. $29^{th}$ European Workshop on Computational Geometry (EuroCG 2013), pages 115-118, Braunschweig, Germany, 2013.