A Note on Planar Monohedral Tilings

O. Aichholzer, M. Kerber, I. Talata, and B. Vogtenhuber

Abstract:

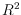
A planar monohedral tiling is a decomposition of $\mathbb{R}^2$ into congruent tiles. We say that such a tiling has the flag property if for each triple of tiles that intersect pairwise, the three tiles intersect in a common point. 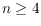We show that for convex tiles, there exist only three classes of tilings that are not flag, and they all consist of triangular tiles; in particular, each convex tiling using polygons with $n\geq 4$ vertices is flag. We also show that an analogous statement for the case of non-convex tiles is not true by presenting a family of counterexamples.

Reference: O. Aichholzer, M. Kerber, I. Talata, and B. Vogtenhuber. A note on planar monohedral tilings. In Proc. $34^{th}$ European Workshop on Computational Geometry EuroCG '18, pages 31:1-31:6, Berlin, Germany, 2018.