Geodesic Order Types

O. Aichholzer, M. Korman, A. Pilz, and B. Vogtenhuber

Abstract:

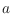
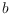
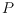
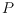
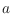
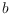
The geodesic between two points $a$ and $b$ in the interior of a simple polygon $P$ is the shortest polygonal path inside $P$ that connects $a$ to $b$. It is thus the natural generalization of straight line segments on unconstrained point sets to polygonal environments. In this paper we use this extension to generalize the concept of the order type of a set of points in the Euclidean plane to geodesic order types. 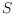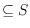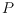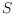In particular, we show that, for any set $S$ of points and an ordered subset $\blue \subseteq S$ of at least four points, one can always construct a polygon $P$ such that the points of $\blue$ define the geodesic hull of $S$ w.r.t. 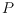$P$, in the specified order. Moreover, we show that an abstract order type derived from the dual of the Pappus arrangement can be realized as a geodesic order type.

Reference: O. Aichholzer, M. Korman, A. Pilz, and B. Vogtenhuber. Geodesic order types. In J. Gudmundsson, J. Mestre, and T. Viglas, editors, Proc. $18^{th}$ International Computing and Combinatorics Conference (COCOON 2012), volume 7434 of Lecture Notes in Computer Science, pages 216-227, Sydney, Australia, August 2012. Springer.