Inserting one edge into a simple drawing is hard

A. Arroyo, F. Klute, I. Parada, R. Seidel, B. Vogtenhuber, and T. Wiedera

Abstract:

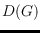
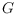
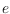
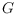
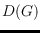
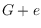
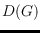
A simple drawing $D(G)$ of a graph $G$ is one where each pair of edges share at most one point: either a common endpoint or a proper crossing. An edge $e$ in the complement of $G$ can be inserted into $D(G)$ if there exists a simple drawing of $G+e$ extending $D(G)$. 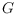As a result of Levi's Enlargement Lemma, if a drawing is rectilinear (pseudolinear), that is, the edges can be extended into an arrangement of lines (pseudolines), then any edge in the complement of $G$ can be inserted. In contrast, we show that it is -complete to decide whether one edge can be inserted into a simple drawing. This remains true even if we assume that the drawing is pseudocircular, that is, the edges can be extended to an arrangement of pseudocircles. 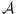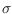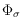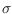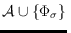On the positive side, we show that, given an arrangement of pseudocircles $\mathcal{A}$ and a pseudosegment $\sigma$, it can be decided in polynomial time whether there exists a pseudocircle $\Phi_\sigma$ extending $\sigma$ for which $\mathcal{A}\cup\{\Phi_\sigma\}$ is again an arrangement of pseudocircles.

Reference: A. Arroyo, F. Klute, I. Parada, R. Seidel, B. Vogtenhuber, and T. Wiedera. Inserting one edge into a simple drawing is hard. In 45th International Workshop on Graph-Theoretic Concepts in Computer Science, Leeds, United Kingdom, 2020.