Graphs with large total angular resolution

O. Aichholzer, M. Korman, Y. Okamoto, I. Parada, D. Perz, A. van Renssen, and B. Vogtenhuber

Abstract:

The total angular resolution of a straight-line drawing is the minimum angle between two edges of the drawing. It combines two properties contributing to the readability of a drawing: the angular resolution, that is the minimum angle between incident edges, and the crossing resolution, that is the minimum angle between crossing edges. We consider the total angular resolution of a graph, which is the maximum total angular resolution of a straight-line drawing of this graph. 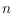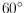We prove that, up to a finite number of well specified exceptions of constant size, the number of edges of a graph with $n$ vertices and a total angular resolution greater than $60^{\circ}$ is bounded by $2n-6$. 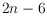This bound is tight. 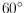In addition, we show that deciding whether a graph has total angular resolution at least $60^{\circ}$ is -hard.

Reference: O. Aichholzer, M. Korman, Y. Okamoto, I. Parada, D. Perz, A. van Renssen, and B. Vogtenhuber. Graphs with large total angular resolution. In Graph Drawing and Network Visualization. GD 2019, volume 11904 of Lecture Notes in Computer Science (LNCS), pages 193-199, Prague, Czechia, 2019.