An optimal algorithm for reconstructing point set order types from radial orderings

O. Aichholzer, V. Kusters, W. Mulzer, A. Pilz, and M. Wettstein

Abstract:

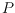
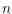
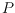
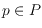
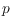
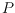
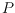
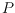
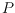
Given a set $P$ of $n$ labeled points in the plane, the radial system of $P$ describes, for each $p\in P$, the radial order of the other points around $p$. This notion is related to the order type of $P$, which describes the orientation (clockwise or counterclockwise) of every ordered triple of $P$. Given only the order type of $P$, it is easy to reconstruct the radial system of $P$, but the converse is not true. Aichholzer et al. (Reconstructing Point Set Order Types from Radial Orderings, in Proc. 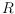ISAAC 2014) defined $T(R)$ to be the set of order types with radial system $R$ and showed that sometimes $\vert T(R)\vert=n-1$. 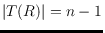They give polynomial-time algorithms to compute $T(R)$ when only given $R$. 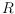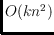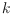We describe an optimal $O(kn^2)$ time algorithm for computing $T(R)$, where $k$ is the number of order types reported by the algorithm. The reporting relies on constructing the convex hulls of all possible point sets with the given radial system, after which sidedness queries on point triples can be answered in constant time. This set of convex hulls can be constructed in linear time. Our results generalize to abstract order types.

Reference: O. Aichholzer, V. Kusters, W. Mulzer, A. Pilz, and M. Wettstein. An optimal algorithm for reconstructing point set order types from radial orderings. In Proceedings $26^{th}$ Int. Symp. Algorithms and Computation (ISAAC 2015), pages 505-516, 2015.