O. Aichholzer, L. Kleist, B. Klemz, F. Schröder, and B. Vogtenhuber
A drawing of a graph in the plane is a
thrackle if every pair of edges
intersects exactly once, either at a common vertex or at a proper crossing.
Conway's conjecture states that a thrackle has at most as many edges as
vertices. In this paper, we investigate the edge-vertex ratio of
maximal thrackles, that is, thrackles in which no edge between already
existing vertices can be inserted such that the resulting drawing remains a
thrackle. For maximal geometric and topological thrackles, we show that the
edge-vertex ratio can be arbitrarily small. When forbidding isolated
vertices, the edge-vertex ratio of maximal geometric thrackles can be
arbitrarily close to the natural lower bound of
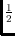
. For maximal
topological thrackles without isolated vertices, we present an infinite
family with an edge-vertex ratio arbitrary close to
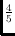
.