Representing Graphs by Polygons with Side Contacts in 3D

E. Arseneva, L. Kleist, B. Klemz, M. Löffler, A. Schulz, B. Vogtenhuber, and A. Wolff

Abstract:

A graph has a side-contact representation with polygons if its vertices can be represented by interior-disjoint polygons such that two polygons share a common side if and only if the corresponding vertices are adjacent. In this work we study representations in 3D. 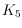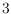We show that every graph has a side-contact representation with polygons in 3D, while this is not the case if we additionally require that the polygons are convex: we show that every supergraph of $K_5$ and every nonplanar $3$-tree does not admit a representation with convex polygons. 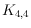On the other hand, $K_{4,4}$ admits such a representation, and so does every graph obtained from a complete graph by subdividing each edge once. 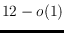Finally, we construct an unbounded family of graphs with average vertex degree $12-o(1)$ that admit side-contact representations with convex polygons in 3D. Hence, such graphs can be considerably denser than planar graphs.

Reference: E. Arseneva, L. Kleist, B. Klemz, M. Löffler, A. Schulz, B. Vogtenhuber, and A. Wolff. Representing graphs by polygons with side contacts in 3D. In Proceedings of the 36th European Workshop on Computational Geometry (EuroCG$\,$2020), Würzburg, Germany, 2020.