Adjacency Graphs of Polyhedral Surfaces

E. Arseneva, L. Kleist, B. Klemz, M. Löffler, A. Schulz, B. Vogtenhuber, and A. Wolff

Abstract:

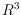
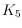
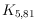
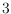
We study whether a given graph can be realized as an adjacency graph of the polygonal cells of a polyhedral surface in $\mathbb{R}^3$. We show that every graph is realizable as a polyhedral surface with arbitrary polygonal cells, and that this is not true if we require the cells to be convex. In particular, if the given graph contains $K_5$, $K_{5,81}$, or any nonplanar $3$-tree as a subgraph, no such realization exists. 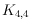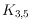On the other hand, all planar graphs, $K_{4,4}$, and $K_{3,5}$ can be realized with convex cells. The same holds for any subdivision of any graph where each edge is subdivided at least once, and, by a result from McMullen et al. (1983), for any hypercube. 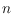Our results have implications on the maximum density of graphs describing polyhedral surfaces with convex cells: The realizability of hypercubes shows that the maximum number of edges over all realizable $n$-vertex graphs is in $\Omega(n \log n)$. 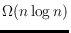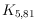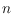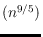From the non-realizability of $K_{5,81}$, we obtain that any realizable $n$-vertex graph has $\bigO(n^{9/5})$ edges. As such, these graphs can be considerably denser than planar graphs, but not arbitrarily dense.

Reference: E. Arseneva, L. Kleist, B. Klemz, M. Löffler, A. Schulz, B. Vogtenhuber, and A. Wolff. Adjacency Graphs of Polyhedral Surfaces. In K. Buchin and E. Colin de Verdière, editors, 37th International Symposium on Computational Geometry (SoCG 2021), volume 189 of Leibniz International Proceedings in Informatics (LIPIcs), pages 11:1-11:17, Dagstuhl, Germany, 2021. Schloss Dagstuhl - Leibniz-Zentrum für Informatik.