The Point Set Order Type Data Base: A Collection of Applications and Results

O. Aichholzer and H. Krasser

Abstract:

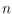
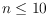
Order types are a common tool to provide the combinatorial structure of point sets in the plane. For many problems in combinatorial and computational geometry only the order type of the underlying point set has to be considered. Recently a complete order type data base of $n$-point sets has been developed for $n\leq 10$, which gives a way to examine the combinatorial properties of all possible point sets for fixed size $n$. 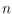Based on this result we present applications and results for problems concerning intersection properties, convexity, crossing-free straight line graphs, and others, thus confirming or disproving several conjectures on these topics. Besides providing concrete results the aim of this work is to stimulate further research by revealing structural relations of extreme examples for $17$ geometrical and combinatorial problems.

Reference: O. Aichholzer and H. Krasser. The point set order type data base: A collection of applications and results. In Proc. $13th$ Annual Canadian Conference on Computational Geometry CCCG 2001, pages 17-20, Waterloo, Ontario, Canada, 2001.