Abstract Order Type Extension and New Results on the Rectilinear Crossing Number

O. Aichholzer and H. Krasser

Abstract:

We extend the order type data base of all realizable order types in the plane to point sets of cardinality 11. More precisely, we provide a complete data base of all combinatorial different sets of up to 11 points in general position in the plane. In addition, we develop a novel and efficient method for a complete extension to order types of size 12 and more in an abstract sense, that is, without the need to store or realize the sets. The presented method is well suited for independent computations. Thus, time intensive investigations benefit from the possibility of distributed computing.
Our approach has various applications to combinatorial problems which are based on sets of points in the plane. This includes classic problems like searching for (empty) convex k-gons ('happy end problem'), decomposing sets into convex regions, counting structures like triangulations or pseudo-triangulations, minimal crossing numbers, and more. We present some improved results to several of these problems. 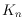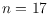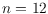As an outstanding result we have been able to determine the exact rectilinear crossing number of the complete graph $K_n$ for up to $n=17$, the largest previous range being $n=12$, and slightly improved the asymptotic upper bound.

Reference: O. Aichholzer and H. Krasser. Abstract order type extension and new results on the rectilinear crossing number. Computational Geometry: Theory and Applications, Special Issue on the 21st European Workshop on Computational Geometry, 36(1):2-15, 2006.