Edge Partitions of Complete Geometric Graphs (Part 2)

O. Aichholzer, J. Obenaus, J. Orthaber, R. Paul, P. Schnider, R. Steiner, T. Taubner, and B. Vogtenhuber

Abstract:

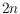
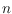
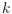
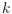
Recently, the second and third author showed that complete geometric graphs on $2n$ vertices in general cannot be partitioned into $n$ plane spanning trees. Building up on this work, in this paper, we initiate the study of partitioning into beyond planar subgraphs, namely into $k$-planar and $k$-quasi-planar subgraphs and obtain first bounds on the number of subgraphs required in this setting.

Reference: O. Aichholzer, J. Obenaus, J. Orthaber, R. Paul, P. Schnider, R. Steiner, T. Taubner, and B. Vogtenhuber. Edge partitions of complete geometric graphs (part 2). 2021.