A note on the number of general 4-holes in perturbed grids

O. Aichholzer, T. Hackl, P. Valtr, and B. Vogtenhuber

Abstract:

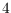
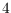
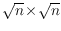
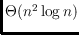
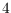
Considering a variation of the classical Erdos and Szekeres type problems, we count the number of general $4$-holes (empty $4$-gons) in the $\sqrt{n}\!\times\!\sqrt{n}$ squared Horton set. 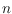Improving on previous upper and lower bounds we show that this number is $\Theta(n^2\log n)$, which also constitutes the currently best upper bound on minimizing the number of general $4$-holes for any set of $n$ points in the plane.
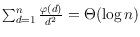
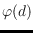
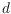
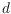
To obtain these bounds and as a result of independent interest, we show that $\sum_{d=1}^n \frac{\varphi(d)}{d^2} = \Theta(\log n)$, where $\varphi(d)$ is Euler's phi-function, the number of positive integers less than $d$ which are relatively prime to $d$.

Reference: O. Aichholzer, T. Hackl, P. Valtr, and B. Vogtenhuber. A note on the number of general 4-holes in perturbed grids. In Proc. $18^{th}$ Japan Conference on Discrete and Computational Geometry and Graphs (JCDCG$^2$ 2015), pages 68-69, Kyoto, Japan, 2015.