Compatible Pointed Pseudo-Triangulations

O. Aichholzer, T. Hackl, and B. Vogtenhuber

Abstract:

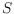
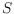
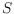
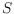
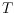
For a given point set $S$ (in general position), two pointed pseudo-triangulations are compatible if their union is plane. We show that for any set $S$ there exist two maximally disjoint compatible pointed pseudo-triangulations, that is, their union is a triangulation of $S$. 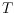In contrast, we show that there are point sets $S$ and pointed pseudo-triangulations $T$ such that there exists no pointed pseudo-triangulation that is compatible to and different from $T$.

Reference: O. Aichholzer, T. Hackl, and B. Vogtenhuber. Compatible pointed pseudo-triangulations. In Proc. $22^{nd}$ Annual Canadian Conference on Computational Geometry CCCG 2010, pages 91-94, Winnipeg, Manitoba, Canada, 2010.