Compatible Matchings for Bichromatic Plane Straight-line Graphs

O. Aichholzer, F. Hurtado, and B. Vogtenhuber

Abstract:

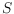
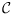
Two plane graphs with the same vertex set are compatible if their union is again a plane graph. We consider bichromatic plane straight-line graphs with vertex set $S$ consisting of the same number of red and blue points, and (perfect) matchings which are compatible to them. 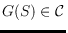For several different classes $\mathcal{C}$ of graphs, we present lower and upper bounds such that any given graph $G(S) \in \mathcal{C}$ admits a compatible (perfect) matching with this many disjoint edges.

Reference: O. Aichholzer, F. Hurtado, and B. Vogtenhuber. Compatible matchings for bichromatic plane straight-line graphs. In Proc. $28^{th}$ European Workshop on Computational Geometry EuroCG '12, pages 257-260, Assisi, Italy, 2012.