On 5-Gons and 5-Holes

O. Aichholzer, T. Hackl, and B. Vogtenhuber

Abstract:

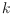
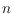
We consider an extension of a question of Erdos on the number of $k$-gons in a set of $n$ points in the plane. Relaxing the convexity restriction we obtain results on 5-gons and 5-holes (empty 5-gons). In particular, we show a direct relation between the number of non-convex 5-gons and the rectilinear crossing number, provide an improved lower bound for the number of convex 5-holes any point set must contain, and prove that the number of general 5-holes is asymptotically maximized for point sets in convex position.

Reference: O. Aichholzer, T. Hackl, and B. Vogtenhuber. On 5-Gons and 5-Holes. In A. Marquez, P. Ramos, and J. Urrutia, editors, Computational Geometry: XIV Spanish Meeting on Computational Geometry, EGC 2011, Festschrift Dedicated to Ferran Hurtado on the Occasion of His 60th Birthday, Alcalá de Henares, Spain, June 27-30, 2011, Revised Selected Papers, volume 7579 of Lecture Notes in Computer Science (LNCS), pages 1-13. Springer, 2012.