Planar L-Shaped Point Set Embedding of Trees

O. Aichholzer, T. Hackl, and M. Scheucher

Abstract:

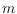
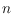
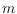
In this paper we consider planar L-shaped embeddings of trees in point sets, that is, planar drawings where the vertices are mapped to a subset of the given points and where every edge consists of two axis-aligned line segments. We investigate the minimum number $m$, such that any $n$ vertex tree with maximum degree 4 admits a planar L-shaped embedding in any point set of size $m$. 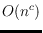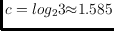First we give an upper bound $O(n^c)$ with $c=log_23 {\approx} 1.585$ for the general case, and thus answer the question by Di Giacomo et al. whether a sub- quadratic upper bound exists. Then we introduce the saturation function for trees and show that trees with low saturation can be embedded even more efficiently. In particular, we improve the upper bound for caterpillars and extend the class of trees that require only a linear number of points. In addition, we present some probabilistic results for either randomly chosen trees or randomly chosen point sets.

Reference: O. Aichholzer, T. Hackl, and M. Scheucher. Planar l-shaped point set embedding of trees. In Proc. $32^{st}$ European Workshop on Computational Geometry EuroCG '16, pages 51-54, Lugano, Switzerland, 2016.