O. Aichholzer, T. Hackl, A. Pilz, P. Ramos, V. Sacristán, and
B. Vogtenhuber
A good drawing of a simple graph is a drawing on the sphere or, equivalently,
in the plane in which vertices are drawn as distinct points, edges are drawn
as Jordan arcs connecting their end vertices, and any pair of edges
intersects at most once. In any good drawing, the edges of three pairwise
connected vertices form a Jordan curve which we call a triangle. We say that
a triangle is empty if one of the two connected components it induces does
not contain any of the remaining vertices of the drawing of the graph. We
show that the number of empty triangles in any good drawing of the complete
graph
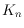
with
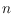
vertices is at least
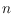
.