Flip Graphs of Bounded-Degree Triangulations

O. Aichholzer, T. Hackl, D. Orden, P. Ramos, G. Rote, A. Schulz, and B. Speckmann

Abstract:

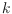
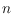
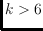
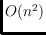
We study flip graphs of triangulations whose maximum vertex degree is bounded by a constant $k$. In particular, we consider triangulations of sets of $n$ points in convex position in the plane and prove that their flip graph is connected if and only if $k > 6$; the diameter of the flip graph is $O(n^2)$. 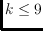We also show that, for general point sets, flip graphs of pointed pseudo-triangulations can be disconnected for $k \leq 9$, and flip graphs of triangulations can be disconnected for any $k$. 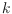Additionally, we consider a relaxed version of the original problem. 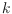We allow the violation of the degree bound $k$ by a small constant. 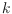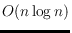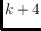Any two triangulations with maximum degree at most $k$ of a convex point set are connected in the flip graph by a path of length $O(n \log n)$, where every intermediate triangulation has maximum degree at most $k+4$.

Reference: O. Aichholzer, T. Hackl, D. Orden, P. Ramos, G. Rote, A. Schulz, and B. Speckmann. Flip graphs of bounded-degree triangulations. Graphs and Combinatorics, 29(6):1577-1593, 2013.