Flip Graphs of Bounded-Degree Triangulations

O. Aichholzer, T. Hackl, D. Orden, P. Ramos, G. Rote, A. Schulz, and B. Speckmann

Abstract:

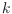
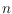
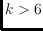
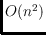
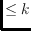
We study flip graphs of triangulations whose maximum vertex degree is bounded by a constant $k$. Specifically, we consider triangulations of sets of $n$ points in convex position in the plane and prove that their flip graph is connected if and only if $k > 6$; the diameter of the flip graph is $O(n^2)$. 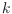We also show that for general point sets, flip graphs of triangulations with degree $\leq k$ can be disconnected for any $k$.

Reference: O. Aichholzer, T. Hackl, D. Orden, P. Ramos, G. Rote, A. Schulz, and B. Speckmann. Flip graphs of bounded-degree triangulations. In Electronic Notes in Discrete Mathematics: Proc. European Conference on Combinatorics, Graph Theory and Applications EuroComb 2009, volume 34, pages 509-513, Bordeaux, France, 2009.