Flips in combinatorial pointed pseudo-triangulations with face degree at most four

O. Aichholzer, T. Hackl, D. Orden, A. Pilz, M. Saumell, and B. Vogtenhuber

Abstract:

In this paper we consider the flip operation for combinatorial pointed pseudo-triangulations where faces have size 3 or 4, so-called combinatorial 4-PPTs. We show that every combinatorial 4-PPT is stretchable to a geometric pseudo-triangulation, which in general is not the case if faces may have size larger than 4. 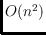Moreover, we prove that the flip graph of combinatorial 4-PPTs with triangular outer face is connected and has diameter $O(n^2)$.

Reference: O. Aichholzer, T. Hackl, D. Orden, A. Pilz, M. Saumell, and B. Vogtenhuber. Flips in combinatorial pointed pseudo-triangulations with face degree at most four. Int'l Journal of Computational Geometry & Applications, 24(3):197-224, 2014.