Plane Spanning Trees in Edge-Colored Simple Drawings of $K_n$

O. Aichholzer, M. Hoffmann, J. Obenaus, R. Paul, D. Perz, N. Seiferth, B. Vogtenhuber, and A. Weinberger

Abstract:

Károlyi, Pach, and Tóth proved that every 2-edge-colored straight-line drawing of the complete graph contains a monochromatic plane spanning tree. It is open if this statement generalizes to other classes of drawings, specifically, to simple drawings of the complete graph. These are drawings where edges are represented by Jordan arcs, any two of which intersect at most once. We present two partial results towards such a generalization. First, we show that the statement holds for cylindrical simple drawings. 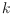(In a cylindrical drawing, all vertices are placed on two concentric circles and no edge crosses either circle.) Second, we introduce a relaxation of the problem in which the graph is $k$-edge-colored, and the target structure must be hypochromatic, that is, avoid (at least) one color class. 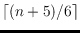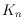In this setting, we show that every $\lceil (n+5)/6\rceil$-edge-colored monotone simple drawing of $K_n$ contains a hypochromatic plane spanning tree. 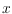(In a monotone drawing, every edge is represented as an $x$-monotone curve.)

Reference: O. Aichholzer, M. Hoffmann, J. Obenaus, R. Paul, D. Perz, N. Seiferth, B. Vogtenhuber, and A. Weinberger. Plane spanning trees in edge-colored simple drawings of $k_n$. In Graph Drawing and Network Visualization (GD 2020), Lecture Notes in Computer Science (LNCS), pages 482-489. Springer International Publishing, 2021.