O. Aichholzer, T. Hackl, S. Lutteropp, T. Mchedlidze, and
B. Vogtenhuber
A directed path whose edges are assigned labels “up”, “down”, “right”, or
“left” is called
four-directional, and
three-directional if
at most three out of the four labels are used. A
direction-consistent
embedding of an
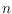
-vertex four-directional path
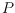
on a set
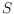
of
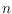
points in the plane is a straight-line drawing of
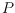
where each vertex
of
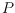
is mapped to a distinct point of
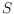
and every edge points to the
direction specified by its label. We study planar direction-consistent
embeddings of three- and four-directional paths and provide a complete
picture of the problem for convex point sets.